Guide to Analytical Model Calculations in the Batoi Insight

Normalizing Values in Batoi Insight

Normalization is a crucial process in data analysis. It allows us to compare variables from different intervals on a common scale. Batoi Insight supports normalizing values into three intervals: [0, 1], [0, 100], and a custom interval [𝑐, 𝑑]

Normalizing to [0, 1] Interval

To normalize a value 𝑥 from an interval [𝑎, 𝑏] to the interval [0, 1], we can use the following formula:

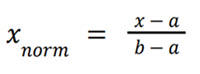
Example Calculation:

Let's say 𝑥 is a value in the interval [1, 5] with 𝑥 = 3.

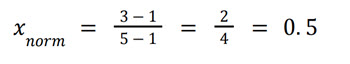
For interval [15, 50] with 𝑥 = 25:

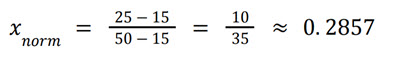
Normalizing to [0, 100] Interval

To normalize a value 𝑥 from an interval [𝑎, 𝑏] to the interval [0, 100], we can use the following formula:

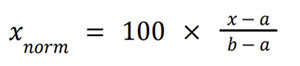
Example Calculation:

For interval 1 − 5:

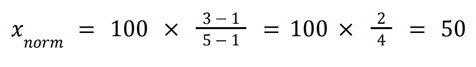
For interval 15 − 50:

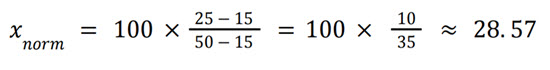
Normalizing to a Default Interval [𝑐, 𝑑]

To normalize a value 𝑥 from an interval [𝑎, 𝑏] to a new interval [𝑐, 𝑑], we can use the following formula:

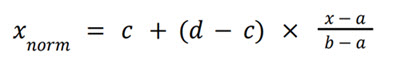
Example Calculation:

Let's assume the default interval is [10, 20].

For interval 1 − 5:

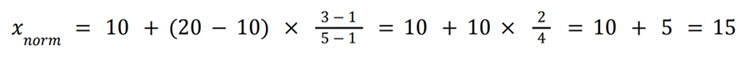
For interval 15 − 50:

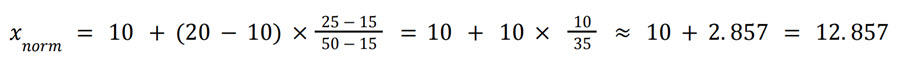
Calculating Weighted Scores and Statistical Tendency

Weighted scores and statistical tendencies are critical for analyzing survey data accurately. Batoi Insight uses these metrics to provide a comprehensive view of survey responses.

Weighted Scores

Each question 𝑞_i in a questionnaire has an associated weight w_i and a score value s_i:

WS_i = w_i . s_i,

where WS_i is the weighted score value for the i-th question. This calculation helps understand each question's relative importance based on its assigned weight.

Statistical Tendency

Statistical tendencies summarize data points and include mean, median, and mode measures. These measures help in understanding the central point around which data values cluster.

For score values:

ST(s_i) = Statistical Central Tendency of score values for the i^th question

For weighted score values:

ST(w_is_i) = Statistical Central Tendency of weighted score values for the i^th question

Group Scores

Group scores aggregate individual responses to provide a higher-level view of data.

For a group g, the score S_g and weighted score WS_g are calculated as:

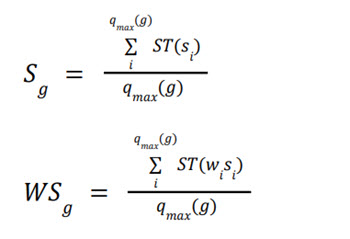
Where q_max(g) is the maximum number of questions accounted for the score in group g.

Adjustment Coefficient

Adjustment coefficients fine-tune the analysis by accounting for specific group characteristics and ensuring accurate data representation.

The final score with adjustment coefficient C_g for group g is:

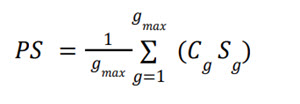
Handling Multiple Score Parameters

If a group has multiple score parameters associated with it, the intra-group statistical operation is defined as:

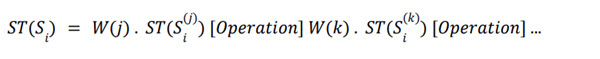
Where W() is the score weight and [𝑂𝑝𝑒𝑟𝑎𝑡𝑖𝑜𝑛] can be +, -, ⋅, /.

Attributes of an Analytical Model

An analytical model in Batoi Insight includes the following attributes:

• Name: The identifier for the model.
• Description (Optional): A brief explanation of the model.
• Normalization: Specifies whether normalization is None, Unity, or Percentage.
• Statistical Tendency: Determines the central tendency measure used (Mode, Mean, Median)

Note: Statistical central tendencies describe the center of a data set or distribution. They summarize the dataset by identifying the central point around which the data values cluster.

Practical Application of Calculations

Let's apply these concepts to a practical example. Suppose we have a questionnaire with the following details:

• The interval for responses: 1 − 5 for one set, 15 − 50 for another.
• Weights assigned to questions.
• Multiple score parameters for specific groups.

We want to normalize the responses, calculate weighted scores, and apply an adjustment coefficient to derive the final score for a group.

1. Normalize the Responses:

For a response 𝑥 = 4 in the interval 1 − 5:

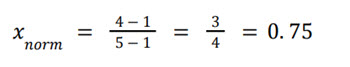
For a response 𝑥 = 30 in the interval 15 − 50:

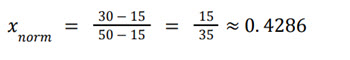
2. Calculate Weighted Scores:

Assume the weights are w₁ = 0.2 and w₂ = 0.3 for two questions with normalized scores s₁ = 0.75 and s₂ = 0.4286

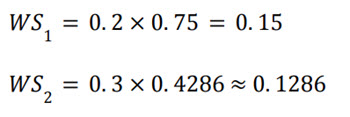
3. Compute Group Scores and Apply Adjustment Coefficient:

Let's assume the adjustment coefficient C_g = 1.1 and the group has two questions:

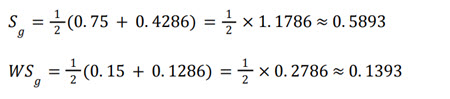
Applying the adjustment coefficient:

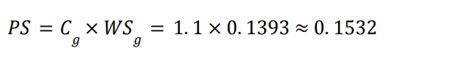
Conclusion

Batoi Insight's robust calculation and normalization features empower users to analyze detailed and accurate survey data. By understanding and utilizing these tools, users can derive valuable insights and make informed decisions based on comprehensive data analysis.

Please refer to our documentation or contact support for further assistance or detailed examples.