Batoi Research Group 
Neural networks are essentially a circuit of neurons, biological or artificial. But of course, we are not going to talk about biological Neural Networks in this article.
An Artificial Neural Network (ANN) is a network of artificial neurons designed to mimic the working of its biological counterpart, the brain. ANNs are a subset of Machine Learning Algorithms which are at the center of deep learning Algorithms. ANNs specialize in various tasks like regression, time series prediction, classification, data compression, and many more.
So far, we have understood that artificial neurons make up the neural network. But what is a neuron? In biology, neurons are cells that fire electrochemical signals when the potential reaches a particular threshold value. The artificial neuron works similarly. Still, structure-wise, this neuron is just a node (like nodes in graph data structures) holding specific numerical values. We will understand how the “firing” of the artificial neurons works further in this article.
In 1943, McCulloch and Pitts gave the first computational model for neurons called the McCulloh-Pitts model.
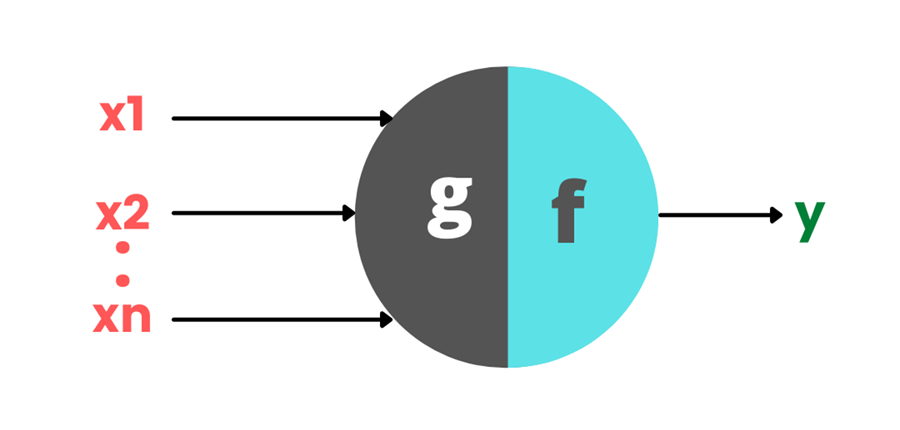
This is the most basic form of the neuron. It gets inputs in the form of \((x_1, x_2, ..., x_n)\). The function, \(g\), sums up all the inputs. Like we had a threshold potential in a biological neuron that made the neuron fire, we also have a threshold value Theta. If the \( sum (x_1 + x_2 + ... + x_n)\) exceeds this value, the neuron outputs a value as \(1\), meaning the neuron fired, and if the sum doesn’t exceed this value, the neuron outputs a value as \(0\), meaning the neuron didn’t fire.
\( \hspace{7em} g(x_1, x_2, x_3, ..., x_n) = g(X) = \sum_{i=1}^n x_i \)
\( \hspace{7em} y = f (g(X)) = 1 \hspace{2em} if \hspace{2em} g(X) \geq \theta \)
\( \hspace{12.3em} = 0 \hspace{2em} if \hspace{2em} g(X) < \theta \)
Any neural network, no matter how complex, is made up of neurons that work similarly. The function \(f\) is called the activation function. The activation function is generally a non-linear function acting on the sum of the inputs \((g(X))\). An example of such an activation function is the sigmoid function. It is one of the most popular activation functions. It is defined by the formula.
\( \hspace{12em} S(X) = \frac {e^X}{(e^x+1)} \)
And it is characterized by an S-shaped curve called the sigmoid curve.
If the value goes above 0.5, the neuron fires else; it doesn’t.
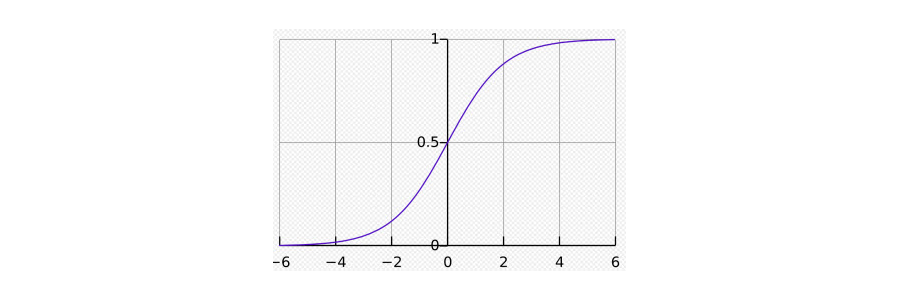
Now that we know about neurons and activation functions let us move on along the topic. NNs are built by stacking a number of these neurons in layers.
As you can see in the image, the NNs are divided into three layers.
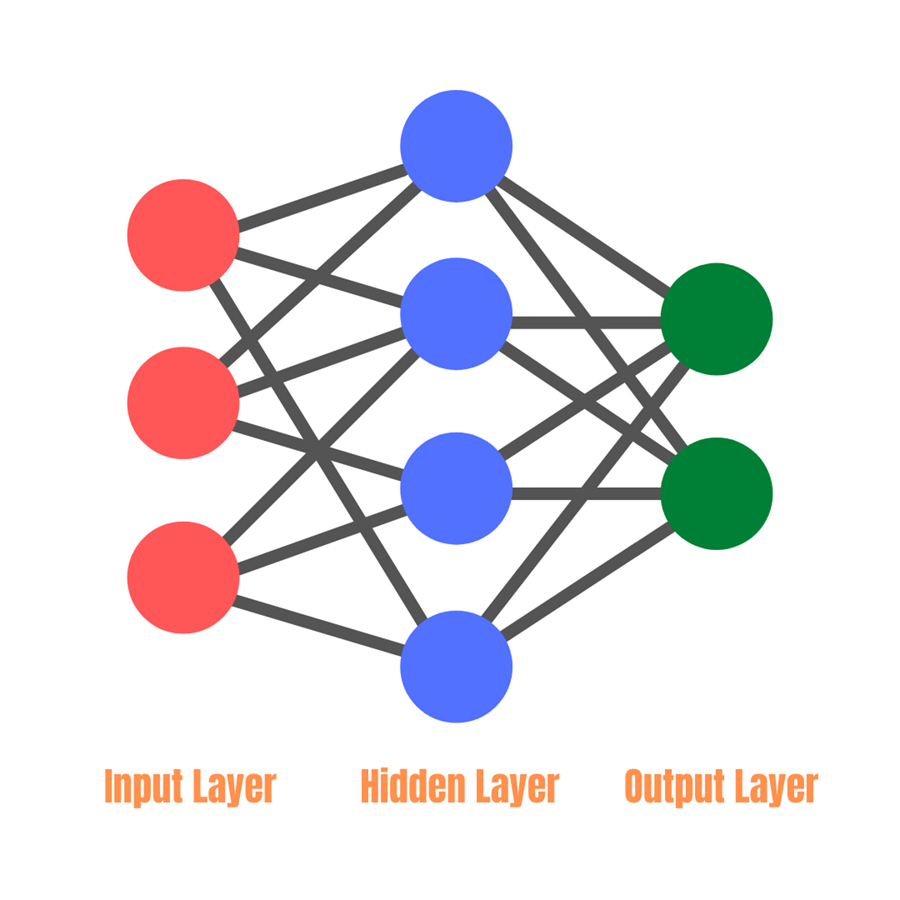
The input layer is the layer where the input is given. Let's say the job of the NN is to recognize if the given image is of a cat or a dog. So, the input layer will be the layer that will receive the image.
The output layer is the layer that makes decisions. The number of neurons in this layer depends on the number of possible outcomes. For instance, here, the NN can give two answers, "It is a dog" or "It is a cat." So, this NN has two neurons in the output layer. The first one becomes "1" whenever the NN sees a dog in the image, and the second one becomes "1" whenever it sees a cat in the image.
Hidden layers are all the layers that come in between the above two layers. How many hidden layers a Neural Net will have and how many neurons each Hidden layer will have is entirely a matter of experiment. Tweaking these values may increase or decrease the performance of the model.
Now the question arises: how does this NN learn to do what it is supposed to do, for example, recognizing cats and dogs.
Every neuron is connected to some/all the neurons from its previous layer. These connections carry some weight. So, when the neuron gets the inputs, it doesn't just calculate the sum of those inputs but the weighted sum of those inputs. And then, this weighted sum passes through the activation function.
These weights are called the hyperparameters whose value the Neural Networks decides itself. How? We will see. An NN, or any AI algorithm in general, can't give a 100% correct answer, rather a very close to correct answer. The model sometimes gives the wrong answer, but the goal is to make the model as accurate as possible and reduce error probability. This is what we call the accuracy of the model. Changing the hyperparameters might increase/decrease the model's accuracy, and the NN, itself, tunes these parameters to that sweet spot over numerous cycles to get maximum accuracy - this signifies the term learning.
To train a neural network, we first build the structure of the model and assign some random values to all the weights. After that, we give input to the NN. The network then provides some output based on the input. We calculate the amount of error that the network has made and then feed this error back to the network. The network, based on this feedback, adjusts its weights. The process is repeated several times until the network’s accuracy is maximized.
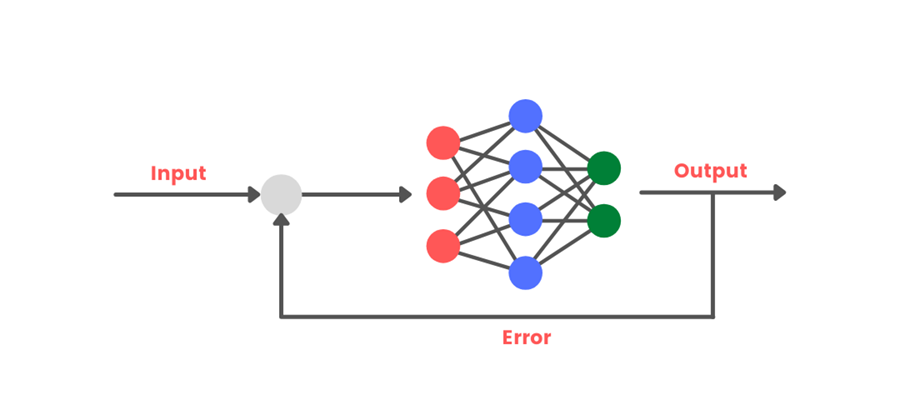
Factors like the number of hidden layers, number of neurons in each layer, choice of activation function, choice of the error function, the training time of the model, the size of the training dataset, etc., also affect the model’s performance. Different values of these parameters are experimented with to get the best results.
