Secure Hash Algorithms

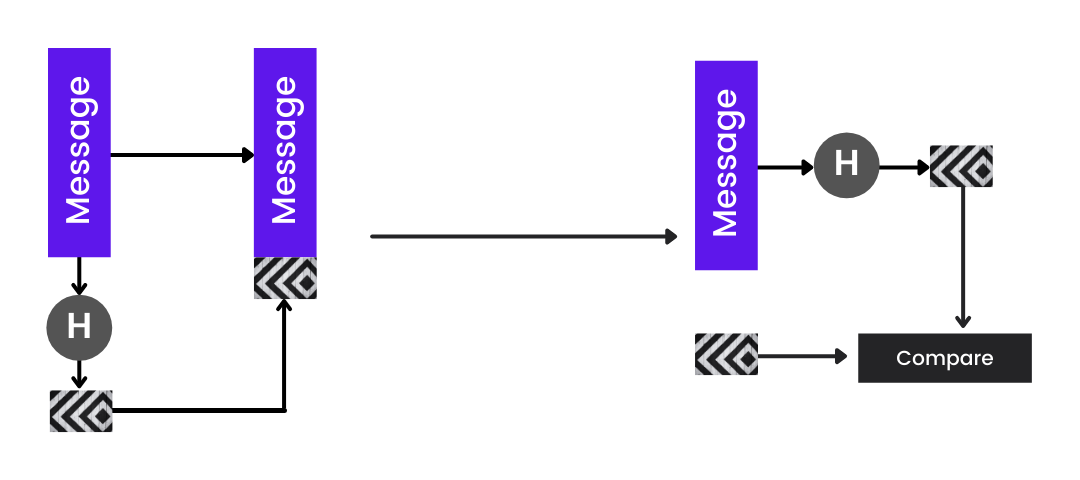
Let’s kick off this article with a scenario. Say we are to send a message to someone named Max. Now, the message that Max will receive must be the identical message that we sent him and is not tampered with during transit. How can we achieve that? For example, if we are going to cash a cheque in real life, the bank needs to be sure that the cheque is authentic. And how do you prove it? You sign it, and they verify against your previously-stored signature. Here also, we use the same trick. We attach a piece of extra information with the document that is called a digital signature.

A digital signature is a cryptographic hash created for a message that is then encrypted along with the entire message to authenticate a digital message or document.

So, What Is a ‘hash’ Anyway?

A hash is a unique, fixed-length string called hash value or message digest obtained by compressing a message or a document by passing it through a mathematical function called a hash function.

When the message reaches the receiver, he/she can decrypt the message, hash the message’s contents using the same hash function, and then compare that hash with the digital signature to authenticate.

You might sometimes confuse between hashing and encryption. The difference is that encryption can be reversed to get the original message (decryption), but a hash can never be reversed.

A Bit of History

Secure Hash Algorithms (SHA) are a family of cryptographic hash functions developed by the National Institute of Standards and Technology (NIST)¹ along with NSA, previously released as a U.S. Federal Information Processing Standard (FIPS) later in 1995; it was named as SHA. It includes four algorithms:

1. SHA0
2. SHA1
3. SHA2
4. SHA3

A typical application of SHA is to encrypt passwords. SHAs show an effect called the avalanche effect. Whenever a small part of the message is changed, the hash value changes drastically. This way, an attacker can’t get any helpful information about the original message using the hash value.

SHA1

SHA0 was a retronym of the original version of a 160-bit hash function called SHA, published in 1993, withdrawn shortly after being issued due to significant flaws. After which came SHA1, a 160-bit or 20-byte hash function, meaning the output was 160 bit long. It is not considered very secure, but many newer hashing algorithms work similarly. So let’s quickly dive in and understand how it works internally.

Working of SHA1

The working of SHA1 is rather interesting. Imagine we have a black box that takes 512 bits of information and gives five 32 bits values. This process goes on and on until the entire message has gone through the box. Finally, the five 32 bits values returned by the box (that is 160 bit) is your hash value. This is how SHA1 works.

Suppose we are trying to hash the string batoi. This string, batoi in binary, is 01110000 01101000 01111001 01110100 01101111 01101111 01101110 (56 bits).

First, we will generate five random 32 bits values. These values are called the initial internal state of the algorithm.

• H0 = 01100111 11011110 00101010 00000001
• H1 = 10111011 00000011 11100010 10001100
• H2 = 00000001 00011110 11110001 11011100
• H3 = 10010010 10010011 11101001 11100010
• H4 = 11001101 11101111 00100011 10101001

After this, the next step will be to pad this string batoi to 512 bits as we saw that SHA1 expects 512 bits at a time. Padding is done by adding a 1 and then adding enough 0s to make the string 448 bits. Finally, the last 64 bits are used to represent the original length of the string.

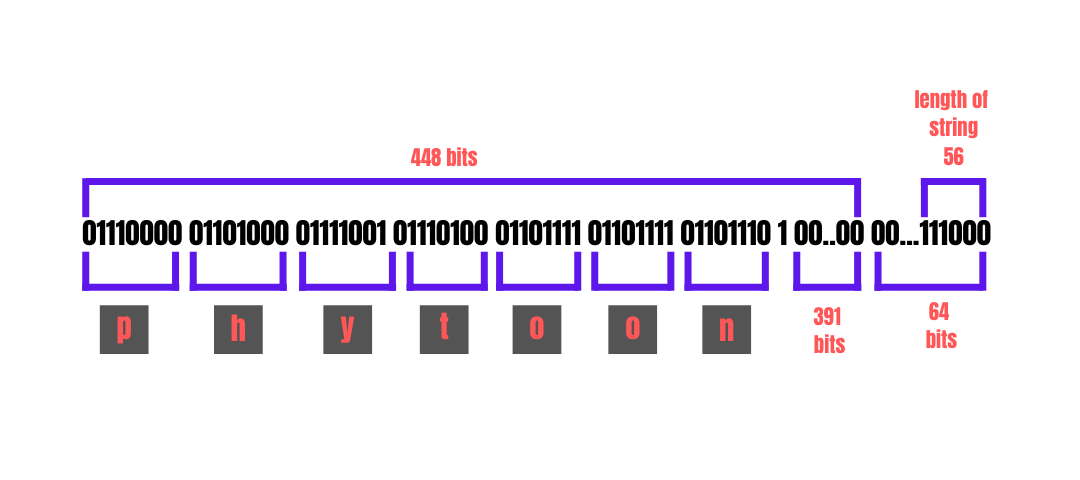
Since our string length was already less than 512 bits, we can now directly pass it to the hash function. If the string was longer, say 5000 bits. It would be broken down into chunks of 512 bits and then passed through the hash function one by one.

We will not get into the actual hash function because mathematics can be hard to understand. After the 512-bit chunk is passed to the hash function, the internal state,i.e., the five H values we chose initially, will change. And it will keep on changing every time a new chunk comes.

Finally, the combination of the five H values will give us the resultant hash value.

Other Hash Algorithms of SHA Family

As we have mentioned earlier, the SHA1 was not the most secure algorithm. Thus, more algorithms were produced due to increasing numbers and levels of vulnerabilities.

SHA2 consists of two identical hash functions called SHA-512 and SHA-256, which consist of differently sized block sizes. Different truncated versions of these hash functions include SHA-224, SHA-384, SHA-512/224, and SHA-512/256.

SHA3 uses a hash function called Keccak². NIST released it in 2005. It supports the same hash lengths as SHA2, and its internal structure differs significantly from the rest of the SHA family.